If, like me, you grew up coding in the 1980s you’ll probably have fond memories of the Mandelbrot Set - it, and other fractals, were everywhere.

I could be wrong but I think I first came across them in a copy of BeeBug, a magazine that I read avidly! In any case I vividly remember watching one slowly, oh so slowly, render on my BBC Model B.

I’ve always found them fascinating and, as simplistic code for rendering for one is pretty straightforward, I’ve implemented them several times. As part of the Game Engine book I’ve been spending a lot of time recently coding shaders and a weekend or two back I suddenly had the urge to implement a Mandelbrot on the GPU in a shader. You can try the results for yourself online. It works best on a laptop with a trackpad with inertial scrolling (like a MacBook) but also works with a mouse wheel quite well.

Mandelbrot’s are really, really, well suited for parallelised number crunching. Essentially to render a Mandelbrot you visit visit each pixel in the frame, figure out which complex number is associated with it, and then perform an iterative / recursive calculation until an escape threshold is reached: either the resulting value exceeds a given threshold or a defined maximum number of iterations has been reached. In the former case the colour is calculated (how this is calculated is completely arbitrary - it has nothing to do with the actual Mandelbrot mathematics) and in the latter case the colour is deemed to be black.

The important thing, from a parallelisation point of view, is that the calculations for each pixel are independent of the calculations for the other pixel. This is perfect for a GPU and even without doing any tricks simply loading this onto a GPU will result in something that performs like that in the video. As an aside you can do many tricks to optimise the calculation of a Mandelbrot - this absolute genius has one rendering in 12 seconds on a BBC and explains how.

So how does it work?

There’s a really nice explanation over here but for our purposes I’m going to try and describe it really concisely and get into the shaders.

The Mandelbrot is the result of the aforementioned iterative calculations performed on a series of complex numbers. Complex numbers extend real numbers to include what is known as an imaginary number usually donated as i. An imaginary number is any number that satisfies the equation i * i = -1 (as in i squared equals - 1). No real number can satisfy that equation.

Complex numbers can be visualised on a plane where, if z is a complex number, then it can be said that z = x + iy. You can probably see where this is going now - the Mandelbrot lives in a range of values on that plane and so to create our visualisation we’re going to set up a range on this plane and feed that to the GPU and, by mapping that plane onto our screen / window (which is what a vertex shader does) we’ll iterate over the plane running our calculations in the fragment shader.

If you want to know more about shaders and how they work you can find an overview in the book currently being serialised on my Patreon: Game Engine Development with C#.

The code I refer to below can be found in GitHub. The host for it is just some pretty basic HTML and JavaScript that wires up some input events, sets up a canvas, gains access to the WebGL context, and kicks off our render.

Our vertex shader (shader.vert) is incredible simple:

#version 300 es
precision mediump float;
in vec4 vertexPosition;

uniform mat4 uModelViewMatrix;
uniform mat4 uProjectionMatrix;

void main(void) {
  gl_Position = uProjectionMatrix * uModelViewMatrix * vertexPosition; // - vec4(0,-0.5,0,0);
}

Even though its simple there are a couple of things worth noting.

Firstly, we’re using version 3 of GLSL ES. This is important and we’ll see why in the fragment shader. Secondly, our projection matrix is an orthogonal matrix - we want our Mandelbrot to be projected in a 2-dimensional manner and our model view is set up such that the two triangles we render form a rectangle that covers the whole canvas. As such when our fragment shader runs its essentially iterating over every screen co-ordinate.

And so onto our fragment shader which is a bit more complex:

#version 300 es
precision highp float;
uniform vec2 uScale;
uniform vec2 uMin;
uniform float maxIterations;
out vec4 fragColor;

const vec3 baseColor0 = vec3(0.0,7.0,100.0) / 255.0;
const vec3 baseColor1 = vec3(32.0,107.0,203.0) / 255.0;
const vec3 baseColor2 = vec3(237.0,255.0,255.0) / 255.0;
const vec3 baseColor3 = vec3(255.0,170.0,0.0) / 255.0;
const vec3 baseColor4 = vec3(0.0,2.0,0.0) / 255.0;

vec3 interpolate(vec3 color1, vec3 color2, float fraction) {  
  return color1 + (color2 - color1) * fraction;
}

// Colour picking could do with some work
vec3 rgbColorFromIteration(float iteration) {
  float fractionalIteration = iteration / maxIterations;
  if (fractionalIteration <= 0.16) return interpolate(baseColor0, baseColor1, fractionalIteration / 0.16);
  if (fractionalIteration <= 0.42) return interpolate(baseColor1, baseColor2, (fractionalIteration - 0.16) / (0.42-0.16));
  if (fractionalIteration <= 0.6425) return interpolate(baseColor2, baseColor3, (fractionalIteration - 0.42) / (0.6425-0.42));
  if (fractionalIteration <= 0.8575) return interpolate(baseColor3, baseColor4, (fractionalIteration - 0.6425) / (0.8575-0.6425));
  return baseColor4;
}

vec3 mandelbrot() {
  vec2 scaled = vec2(gl_FragCoord.x * uScale.x + uMin.x, gl_FragCoord.y * uScale.y + uMin.y);
  vec2 c = vec2(0.0,0.0);

  for (float iteration=0.0; iteration < maxIterations; iteration++) {
    if (dot(c,c) > 4.0) return rgbColorFromIteration(iteration);
    c = vec2(c.x*c.x - c.y*c.y + scaled.x, 2.0 * c.x * c.y + scaled.y);        
  }
  return vec3(0,0,0);
}

void main(void) {
  fragColor = vec4(mandelbrot(), 1);
}

For us to be able to run our calculations we pass a few parameters into the shader:

uScale - the current zoom level uMin - the top left position on the complex plane we need to render maxIterations - the maximum number of iterations before stopping our calculations

The top half of the shader handles the colour selection - essentially we use the number of iterations to select a colour from a pre-determined palette.

The Mandelbrot calculation is handled in the mandelbrot() function and this is the reason we’re using GLSL ES 3.0. Previous versions of GLSL required for loops to have a constant as their terminator - this is because GPUs like to unbundle the loops. GLSL ES 3.0 added the capability to use none-constant terminators as we have here. Note - you can write a Mandelbrot on an older GLSL version, you simply can’t pass the maximum number of iterations in as a value and have to restructure the code slightly.

Again, this calculation is going to run for every pixel on the screen - and we don’t need a uMax as an input because that’s essentially defined by uMin + screenSize * uScale. We just need to know where to start. We can determine which pixel is being rendered by the fragment shader by using glFragCoord which is a global that tells us exactly this. And by combining this with uMin and uScale we know where on the complex plane we are.

There are just a couple of things worth noting about the JavaScript wrapper. To support touch gestures (you can pinch on a touch screen) I used a handy library called ZingTouch and the vector and matrix maths used alongside WebGL come from the glmatrix library.

And that’s it really. Pretty simple. A GPU powered Mandelbrot.

That said… I couldn’t help but implement the same algorithm on a BBC (I used an emulator, though I do have a real BBC Master 128) using BBC BASIC to see how long it would take. I left colour selection out and used a low resolution mode (160x256) and you can see the code below:

10 MODE 2
20 VDU 23,1,0;0;0;0;
30 GCOL 0,1
40 XMIN = -2.1
50 XMAX = 0.9
60 XSTEP = (XMAX-XMIN)/1280.0
70 YMIN = -1.0
80 YMAX = 1.0
90 YSTEP = (YMAX-YMIN)/1024.0
100 FOR X=0 TO 1280 STEP 8
110     FOR Y = 0 TO 512 STEP 4
120         MX=0
130         MY=0
140         SCALEDX = X * XSTEP + XMIN
150         SCALEDY = Y * YSTEP + YMIN
160         CX = 0.0
170         CY = 0.0
180         ITERATION = 0
190         PCOLOR = 0
200         REPEAT
210             IF ((MX*MX) + (MY*MY)) > 4.0 THEN PCOLOR = 1
220             MXTEMP = MX*MX - MY*MY + SCALEDX
230             MY = 2*MX*MY + SCALEDY
240             MX = MXTEMP
250             ITERATION = ITERATION + 1
260         UNTIL PCOLOR <> 0 OR ITERATION > 50
270         IF PCOLOR <> 0 THEN PLOT 69,X,Y : PLOT 69,X,1023-Y
280         MY = MY + YSTEP
290     NEXT
300     MX = MX + XSTEP
310 NEXT

Which resulted in the following Mandelbrot:

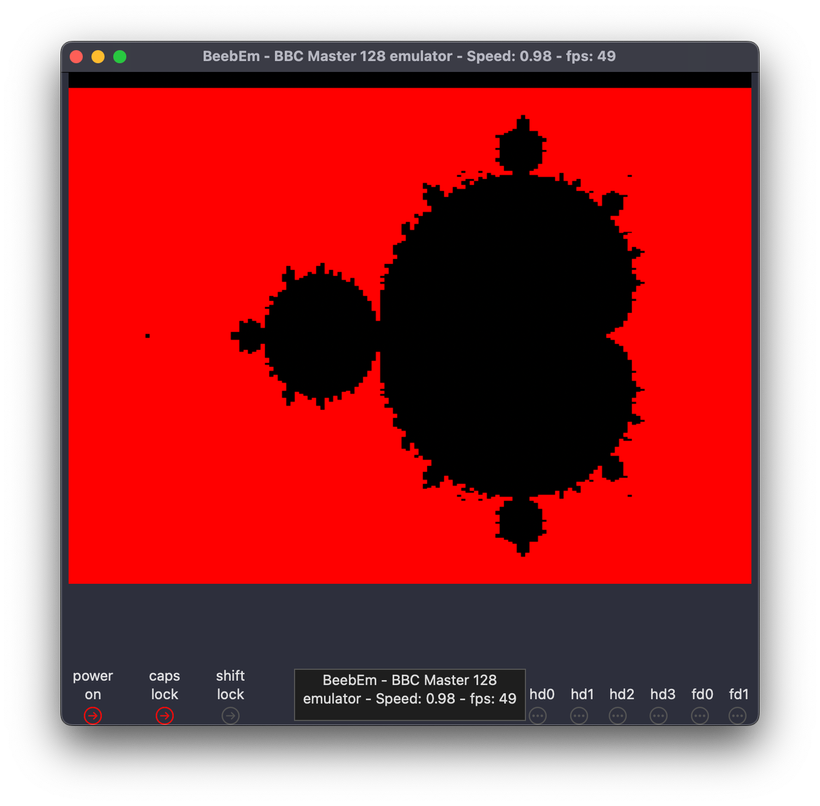
Even though I cheated a little (I knew I wouldn’t be zooming and that the Mandelbrot is symmetrical and so I only calculated half the height of the screen and mirrored it) and is running in such a low resolution it took over 1 hour to generate this.

That said as I mentioned earlier someone has done far far far better than this (12 seconds for a coloured Mandelbrot). Its still remarkable though as a sense of how much faster hardware has got: on my M1 Max MacBook the GPU was rendering this at 60fps+ in basically 4K resolution without skipping a beat.

Incredible really.